反向传播
举个例子
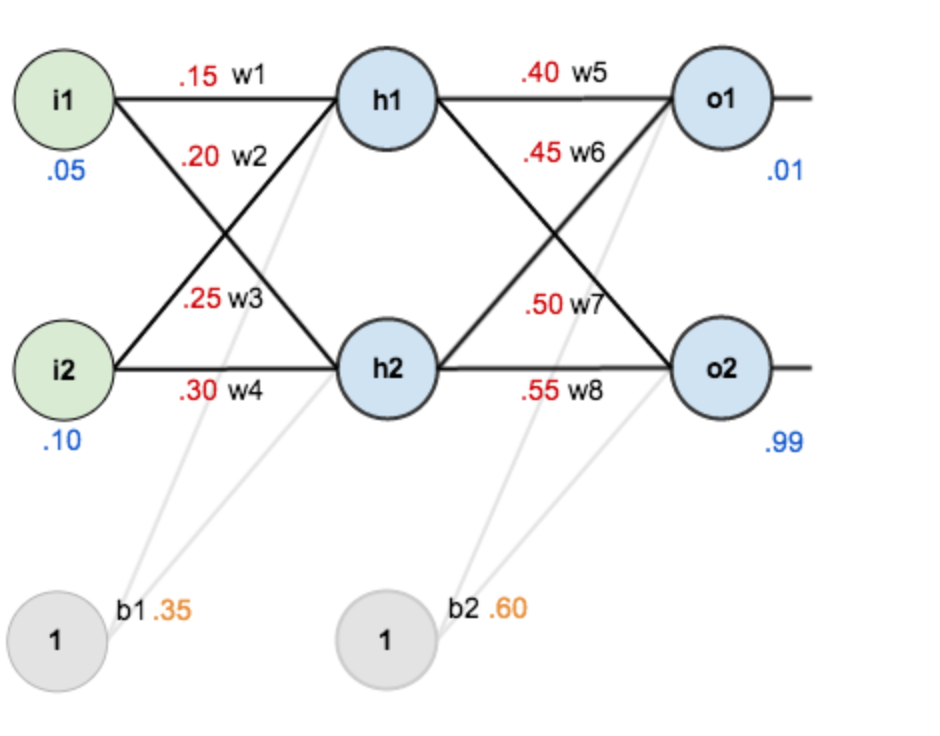第一层是输入层，包含两个神经元i1，i2，和截距项b1；第二层是隐含层，包含两个神经元h1,h2和截距项b2，第三层是输出o1,o2，每条线上标的wi是层与层之间连接的权重，激活函数我们默认为sigmoid函数。
1
2
3
4其中，输入数据 i1=0.05，i2=0.10;
输出数据 o1=0.01,o2=0.99;
初始权重 w1=0.15,w2=0.20,w3=0.25,w4=0.30;
w5=0.40,w6=0.45,w7=0.50,w8=0.55
目标：给出输入数据i1,i2(0.05和0.10)，使输出尽可能与原始输出o1,o2(0.01和0.99)接近。
1.前向传播（输入层-隐含层）
计算神经元h1的输入加权和： $$ out_{h_{i}}=\sigma(w_{i}*i_{i} + w_{i}*i_{i} + b_{i}*1) $$ 则计算结果分别为： $$out_{h1}=0.593269 $$ $$out_{h2}=0.596884 $$
前向传播（隐含层-输出层）
同样的方法$$ out_{o_{j}}=\sigma(w_{j}*out_{h_{j1}} + w_{j}*out_{h_{j2}} + b_{j}*1) $$ 则计算结果为： $$out_{o1}=0.751365 $$ $$out_{o2}=0.772928 $$ 这样前向传播的过程就结束了，我们得到输出值为[0.751365, 0.772928]，与实际值[0.01， 0.99]相差还很远，现在我们对误差进行反向传播，更新权值，重新计算输出。
2.反向传播
计算总误差(均方误差)
$$ E_{total} = \sum\frac{1}{2}(target-output)^{2} $$所以$$E_{total}=E_{o1}+E_{o2}=0.274811+0.023561 = 0.298371 $$
隐含层的权重更新
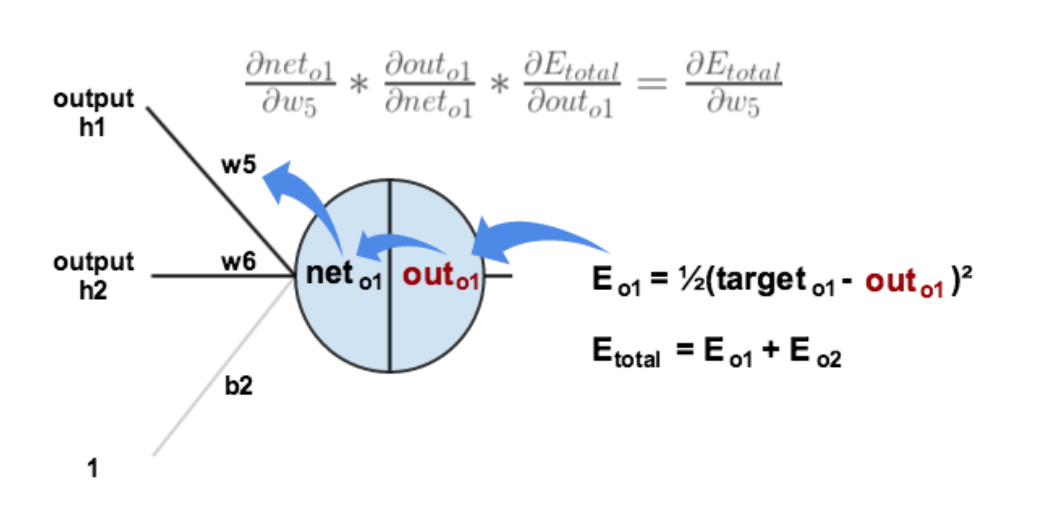
以权重$w_{5}$为例，如果我们想知道$w_{5}$对整体误差产生了多少影响，可以用整体误差对$w_{5}$求偏导求出（链式法则）：
$$\frac{\partial E_{ total}}{\partial w_{5}}=\frac{\partial E_{total}}{\partial out_{w_{5}}}*\frac{\partial out_{w_{5}}}{\partial w_{5}}$$
接下来是复合函数求导，先对sigmoid求导，在对$w_{5}$求导。最终我们得到的结果是：
$$\frac{\partial E_{ total}}{\partial w_{5}}=-(target_{o1}-out_{o1})out_{o1}(1-out_{o1})out_{h1}$$总结一下就是：误差激活函数梯度上一层的输出值,为了表示方便，我们用$\delta_{o1}$来表示输出层的误差，$$ \delta_{o1} = -(target_{o1}-out_{o1})*out_{o1}(1-out_{o1}) $$ $$ \frac{\partial E_{ total}}{\partial w_{5}}=\delta_{o1}out_{h1} $$
最后我们来更新$w_{5}$的值：$$ w_{5}^{+} = w_{5} - \eta\frac{\partial E_{ total}}{\partial w_{5}}=0.4-0.010.082167=0.358916 $$这里$\eta=0.01$，表示学习率，同理，可以更新所有的$w$值。
重复迭代次数可以使得总误差越来越接近真实值。
梯度下降
1.先做一道数学题
用最速下降法求解无约束非线性规划问题，$$ minf(X)= x_{1}-x_{2}+2x_{1}^{2}+2x_{1}x_{2}+x_{2}^{2} $$,其中$X=(x_{1},x_{x2})^\mathrm{T}$，要求选取初始点$X^{1}=(0,0)^\mathrm{T}$，终止误差$\varepsilon=0.5$ 解：目标函数的梯度$\nabla f(x)=\begin{bmatrix} \frac{\partial f(x)}{\partial x_{1}} \ \frac{\partial f(x)}{\partial x_{2}} \end{bmatrix} = \begin{bmatrix} 1+4x_{1}+2x_{2} \ -1+2x_{1}+2x_{2} \end{bmatrix}$, $\nabla f(X^{1})=\begin{bmatrix} 1 \ -1 \end{bmatrix}$令搜索方向$d^{1}=-\nabla f(x^{1})$,再从$X^{1}$出发，沿着$d^{1}$方向作一维寻优，令步长变量为$\lambda$,最优步长为$\lambda_{1}$,则有$$ X^{1}+\lambda d^{1}= \begin{bmatrix} 0 \ 0 \end{bmatrix} + \lambda \begin{bmatrix} -1 \ 1 \end{bmatrix}=\begin{bmatrix} -\lambda \ \lambda \end{bmatrix}$$, 故有$f(x)=f(X^{1}+\lambda d^{1})=(-\lambda)-\lambda + 2(-\lambda)^2+2(-\lambda)\lambda + \lambda ^{2}=\lambda ^{2}-2\lambda=\varphi_{1}(\lambda)$,令$\varphi_{1}(\lambda)=0$可得，$\lambda_{1}=1$,则$X^{2}=X^{1}+\lambda_{1}d^{1}=\begin{bmatrix} -1 \ 1 \end{bmatrix}$,求出$X^{2}$之后，与上类似地，进行第二次迭代：$\nabla f(X^{2})= \begin{bmatrix} -1 \ 1 \end{bmatrix}$，令$d^{2}=-\nabla f(X^{2})$，令步长变量为$\lambda$，求出最优步长$\lambda_{2}$，固有$f(x)=f(X^{2}+\lambda d^{2})=0$,求得$\lambda_{2}=\frac{1}{5}$, 同理：$X^{3}=X^{2}+\lambda_{2}d^{2}=\begin{bmatrix} -0.8 \ 1.2 \end{bmatrix}$,此时$\nabla f(X^{3})=\begin{bmatrix} 0.2 \ -0.2 \end{bmatrix}$,此时所达到的精度$\begin{Vmatrix} \nabla f(X^{3}) \end{Vmatrix}\approx 0.2828$,故此题的最优解$X^{}=\begin{bmatrix} -1 \ 1.5 \end{bmatrix}$,$f(X^{})=-1.25$
从上述题目中可以总结梯度下降法的一般迭代步骤：
- 先确定向下一步的步伐大小，我们称为Learning rate；
- 任意给定一个初始值；
- 确定一个向下的方向，并向下走预先规定的步伐，并更新初始值；
- 当下降的高度小于某个定义的值，则停止下降；
更新初始值的方法：$\theta^{n+1}=\theta^{n}-\eta\nabla C(\theta^{n})$
2.梯度下降原理
导数的概念：$$ f'(x_{0})= \lim_{\Delta x \to 0}\frac{\Delta y}{\Delta x} = \lim_{\Delta x \to 0}\frac{f(x_{0}+\Delta x) - f(x_{0})}{\Delta x} $$，由公式可见，对点$x_{0}$的导数反应了函数在点$x_{0}$处的瞬时变化率，或者叫斜率，推广到多维函数中，就有了梯度的概念，梯度是一个向量组合，反映了多维图形中变化速率最快的方向。
补充（tensorflow中常用的优化算法API）
1
2
3
4
5
6
7
8
9
10
11tf.train.Optimizer
tf.train.GradientDescentOptimizer
tf.train.AdadeltaOptimizer
tf.train.AdagradOptimizer
tf.train.AdagradDAOptimizer
tf.train.MomentumOptimizer
tf.train.AdamOptimizer
tf.train.FtrlOptimizer
tf.train.ProximalGradientDescentOptimizer
tf.train.ProximalAdagradOptimizer
tf.train.RMSPropOptimizer
1、 tf.train.GradientDescentOptimizer
这个优化器主要实现的是:梯度下降算法
1
2
3
4
5__init__(
learning_rate,
use_locking=False,
name='GradientDescent'
)
2、 tf.train.MomentumOptimizer
实现动量梯度下降算法,可参考 简述动量Momentum梯度下降
1
2
3
4
5
6
7__init__(
learning_rate,
momentum,
use_locking=False,
name='Momentum',
use_nesterov=False
)
3、tf.train.AdamOptimizer
实现 Adam优化算法（Adam 这个名字来源于 adaptive moment estimation，自适应矩估计。）可参考博客梯度优化算法Adam
1
2
3
4
5
6
7
8__init__(
learning_rate=0.001,
beta1=0.9,
beta2=0.999,
epsilon=1e-08,
use_locking=False,
name='Adam'
)