CTC
传统的语音识别的模型中，我们对语音模型进行训练之前，往往都要将文本与语音进行严格的对齐操作。这样就有两点不太好：
- 严格对齐要花费人力、时间
- 严格对齐之后，模型预测出的label只是局部分类的结果，而无法给出整个序列的输出结果，往往要对预测出的label做一些后处理才可以得到我们最终想要的结果
CTC是计算一种损失值，主要的优点是可以对没有对齐的数据进行自动对齐($\epsilon$表示'blank')
CTC的概念公式
1.序列问题形式化
序列问题可以形式化为如下函数： $$\mathcal{N}_w: (\mathcal{R}^m)^T \rightarrow (\mathcal{R}^n)^T$$ 其中，序列目标为字符串（词表的大小 $n$），即 $\mathcal{N}_w$ 为出为 $n$ 维多项概率分布（e.g. 经过 softmax 处理）。 网络输出为： $y = \mathcal{N}_w$，其中， $y_k^t$ 表示 $t$ 时刻第 $k$ 项的概率。 虽然没有限定 $\mathcal{N}_w$ 的形式，一般序列建模为神经网络模型RNN。
2. 从网络输出到标签 （Output to Labellings）
音频特征经过RNN的输出为 $y =[ T, V ]$ ， $T$ 表示时间序列，也就是帧数， $V$ 表示所有音素的维度。然后用 $y_k^t$ 表示 $t$ 时刻输出标签为 $k$ 的概率，那么一条路径 $\pi = (\pi_1, \pi_2...\pi_t)$ 的输出概率为： $$p(\pi|x) = \prod_{t=1}^T y_{\pi_t}^t$$ 因为路径与最后的输出标签是多对一的关系，所以定义： $$p(l|x) = \sum_{\pi \in \mathcal{B}^-1(l)} p(\pi|x)$$ 其中 $\mathcal{B}^-1(l)$ 表示所有经过 $B$ 映射变换后得到最终label的路径。 我们的目标就是计算出最大的 $p(l|x)$ 。
3. 多路径映射 $B$
在现实之中，多个路径会对应一个正确的序列，所以定义映射 $B$ ，操作如下：
- 合并连续的相同符号
- 去掉 blank 字符
例如： $B(a-ab-) = B(-aa--abb)=aab$ 。 并且这个序列长度往往小于路径长度，那么序列最终的概率可以使用路径的概率之和表示： $$p(l|x) = \sum_{\pi \in \mathcal{B}^-1(l)} p(\pi|x)$$ ,其中 $\mathcal{B}^-1(l)$ 表示长度为 $T$ 且经过 $B$ 结果为 $l$ 的字符串集合。
4. 构造分类器
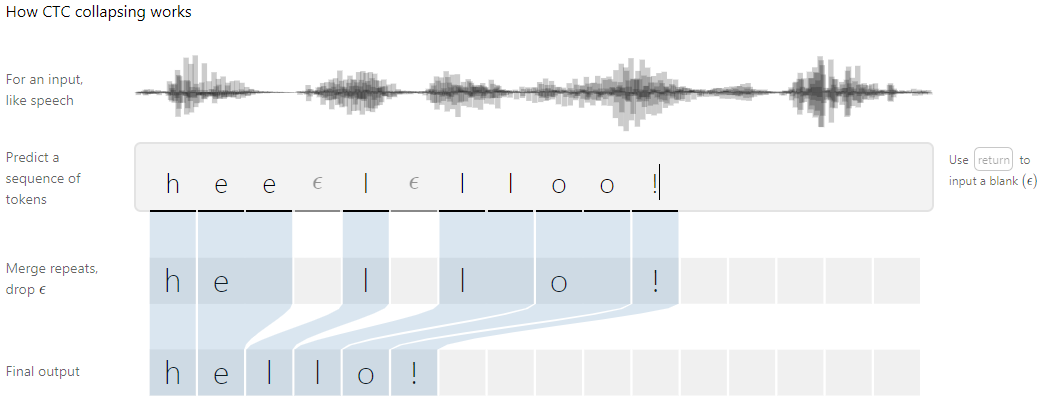
让我们再确定一下我们的目标，我们的目标是通过输入序列 $x$ 得到输出序列 $y$ ，如果我们可以获得输出序列的分布 $p(l|x)$ ，选择其中概率最大的那一个作为「输出序列」即可。这个逻辑可以通过下面公式表示：
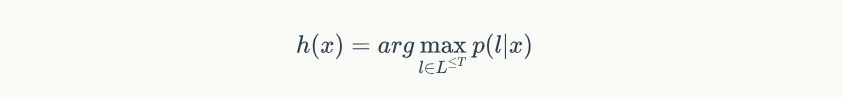
5. 训练和Loss
CTC的loss函数定义如下： $$L(S)=-ln \coprod_{(x,l)\in S}p(l|x)=-\sum_{(x,l)\in S}ln p(l|x)$$ 式中 $S$ 表示的是训练集，那么我需要的就是找到一种高效的方法来计算 $p(l|x)$ 的最大值？
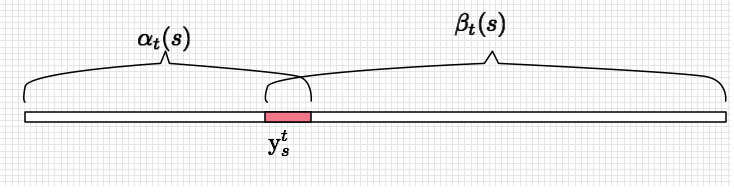
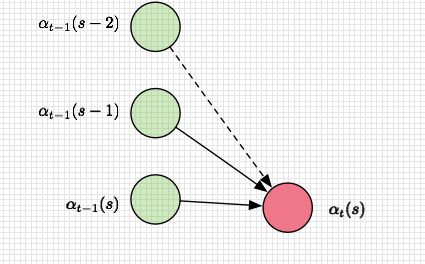
使用 前向后向算法 可以高效计算出 $p(l|x)$ , 使用递推公式可以计算出前向概率 $\alpha_{t}(s)$ ,表示从 $1 \to t$ 时刻之前，所有 $l_{1} \to s$ 个输出的概率，公式为:
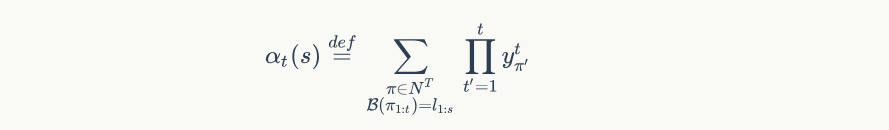同理使用递推公式计算出后向概率 $\beta_{t}(s)$ ，表示所有从 $t \to T$ 输出标签为 $s \to |l|$ 的概率，公式为:
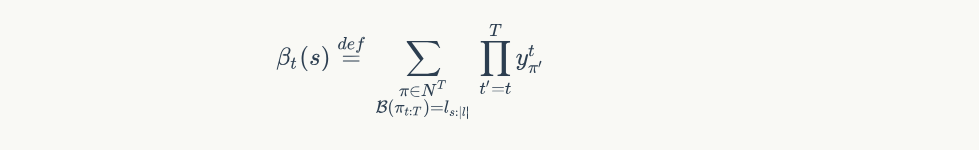得到前向和后向概率，就可以计算出 $p(l|x)$ 的概率
公式：
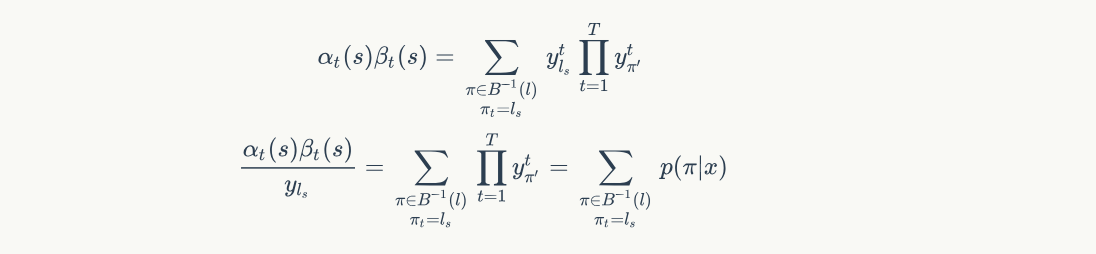所以 $p(l|x)$ 可以表示每个时刻输出label音素的概率之和
$$p(l|x) = \sum_{\pi \in B^{-1}(l)}p(\pi|x) = \sum_{s=1}^{|l^{'}|} \frac{\alpha_t(s)\beta_t(s)}{y_{l_s}^t}$$
6、前向后向概率
6.1 前向概率
数学定义：
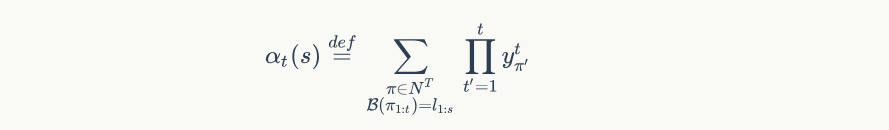这样定义之后，显然会有如下的初始化：
$$\alpha_1(1) = y_b^1$$
$$\alpha_1(2) = y_{l_1}^1$$
$$\alpha_1(s) = 0, \forall s > 2$$
即 $t = 1$ 时只可能有以下情况:
- 输出 $b$ (blank) 的概率为 $y_b^1$
- 输出 $l_1$，即 输出真实标签中的第一个的概率 $y_{l_1}^1$
- 输出标签其他的概率为 0
有了初始化，就可以列出递推公式：
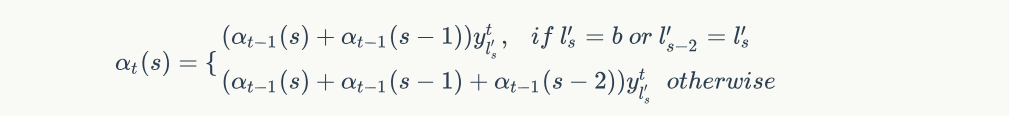解释如下：
6.2 后向概率
后向概率与前向概率一样，定义稍有不同：
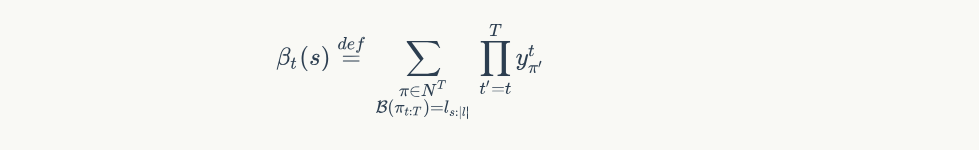则有以下初始化定义( $|l_{'}|$ 表示加了 $b$ (blank)之后的标签长度 )：
$$\beta_T(|l^\prime|) = y_b^T$$
$$\beta_T(|l^\prime|-1) = y_{l_l}^T$$
$$\beta_T(s) = 0, \forall s < |l^\prime| - 1$$
即 $t=T$ 时刻，只有以下的概率输出:
- 输出 $b$ 的概率 $y^{T}_{b}$
- 输出 $|l^{'}|-1$ 即不加 $b$ 的真实标签的最后一个的概率 $y^T_{l_{|l|}}$
- 输出其他概率为 0
后向概率的递推关系:
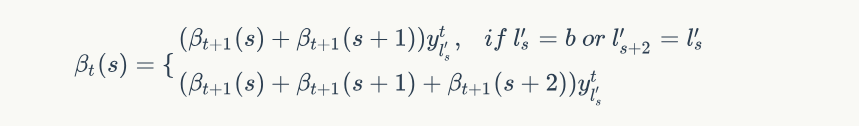解释如下：
7、计算过程
根据递推关系式可以得到如下结果：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50# y表示RNN的特征输出， labels是带空格的
# 例如：labels = [0, 3, 0, 3, 0, 4, 0] # 0 for blank
# y的shape=[T, V], labels的长度L=len(label) + len(blank)
# 通常来说，L = 2*len(label) + 1
def forward(y, labels):
T, V = y.shape
L = len(labels)
alpha = np.zeros([T, L])
# init
alpha[0, 0] = y[0, labels[0]]
alpha[0, 1] = y[0, labels[1]]
for t in range(1, T):
for i in range(L):
s = labels[i]
a = alpha[t - 1, i]
if i - 1 >= 0:
a += alpha[t - 1, i - 1]
if i - 2 >= 0 and s != 0 and s != labels[i - 2]:
a += alpha[t - 1, i - 2]
alpha[t, i] = a * y[t, s]
return alpha
def backward(y, labels):
T, V = y.shape
L = len(labels)
beta = np.zeros([T, L])
# init
beta[-1, -1] = y[-1, labels[-1]]
beta[-1, -2] = y[-1, labels[-2]]
for t in range(T - 2, -1, -1):
for i in range(L):
s = labels[i]
a = beta[t + 1, i]
if i + 1 < L:
a += beta[t + 1, i + 1]
if i + 2 < L and s != 0 and s != labels[i + 2]:
a += beta[t + 1, i + 2]
beta[t, i] = a * y[t, s]
return beta
这样每个时刻每个音素的前向和后向概率就计算好了。接下来计算每个时刻每个因素的梯度，即计算梯度:
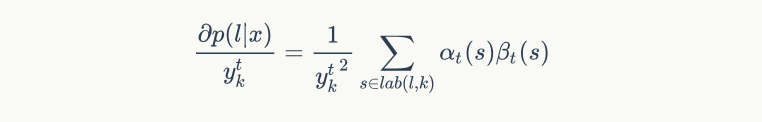其中 $lab(s)={s: l_s^\prime = k}$ ,表达的意思是所有 $l_s=k$ 的 $s$ 的集合，因为满足条件的地方都是潜在的 $y_t^k$ 的概率贡献方。
一般我们优化似然函数的对数，因此，梯度计算如下:
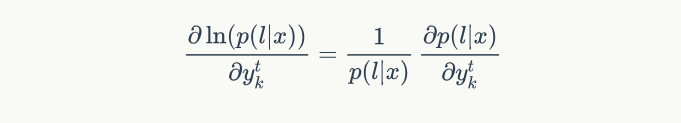其中，似然值在前向计算中已经求得，就是最后输出为 blank 或者 最后一个 $|l^{'}|$ 的前向概率值: $p(l|x) = \alpha_T(|l^\prime|) + \alpha_T(|l^\prime|-1)$ 。这样就可以根据前向后向概率计算出 $y=[T, V]$ 的所有梯度值，有了梯度值，就可以用梯度优化算法进行更新。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20# y是RNN的输入， labels为加空格的标签
def gradient(y, labels):
T, V = y.shape
L = len(labels)
alpha = forward(y, labels)
beta = backward(y, labels)
p = alpha[-1, -1] + alpha[-1, -2]
grad = np.zeros([T, V])
for t in range(T):
for s in range(V):
# 输出 s = l 标签的集合
lab = [i for i, c in enumerate(labels) if c == s]
for i in lab:
grad[t, s] += alpha[t, i] * beta[t, i]
grad[t, s] /= y[t, s] ** 2
grad /= p
return grad
8、解码
8.1 贪心解码(greedy search)
最优路径即为最优输出：hexo
$$h(x) \approx B(\pi^\star) \
\pi^\star = \underset{\pi \in N^T}{argmax}\ p(\pi|x)$$
简化后，解码过程（构造 $π^\star$）变得非常简单（基于独立性假设）： 在每个时刻输出概率最大的字符:
$$\pi^\star = cat_{t=1}^T(\underset{s \in L^\prime}{argmax}\ y^t_s)$$
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19# 输出删除blank
def remove_blank(labels, blank=0):
new_labels = []
# e.g. [-,a,a,-,-,p,p,-,-,p,p,-,-,l,l,-,e,e,-,]
# combine duplicate
previous = None
for l in labels:
if l != previous:
new_labels.append(l)
previous = l
# remove blank
new_labels = [l for l in new_labels if l != blank]
return new_labels
# 贪心搜索
def greedy_decode(y, blank='-'):
raw_rs = np.argmax(y, axis=1)
rs = remove_blank(raw_rs, blank)
return raw_rs, rs
8.2 束搜索 (beam search)
贪心搜索的性能非常受限。例如，它不能给出除最优路径之外的其他其优路径。很多时候，如果我们能拿到nbest的路径，后续可以利用其他信息来进一步优化搜索的结果。束搜索能近似找出 top 最优的若干条路径。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19def beam_decode(y, beam_size=10):
T, V = y.shape
log_y = np.log(y)
beam = [([], 0)]
for t in range(T): # for every timestep
new_beam = []
for prefix, score in beam:
for i in range(V): # for every state
new_prefix = prefix + [i]
new_score = score + log_y[t, i]
new_beam.append((new_prefix, new_score) \ \ )
# top beam_size
new_beam.sort(key=lambda x: x[1], reverse=True)
beam = new_beam[:beam_size]
return beam
8.3 前缀束搜索（Prefix Beam Search）（还没有看明白）
9. 错误率LER (Label Error Rate)
字母定义 $x$ 表示输入序列， $z$ 表示标签序列(label)， $h:x\to z$ 为分类器。 $$ LER(h,S^{'}) = \frac{1}{Z}\sum_{(x,z)\in S}ED(h(x),z) $$ $ED$ 表示编辑距离。
总结
采用CTC端到端训练，就是采用前向后向算法，计算出 $p(l|x)$ 的最大值，这样 $loss = -ln \ \ p(l|x)$ 就是最小值，计算出输出便签概率的梯度，就可以使用梯度下降法做优化，优化的结果使得RNN的输出 $y$ 的解码结果 $h(x)$ 与加了 $b$ 的标签越来越接近，最后的输出删除 $b$ 后的结果。
大致步骤：
- CNN + RNN 特征提取，得到 $y = [帧数，音素数]$
- 计算 $p(l|x)$ ，优化使之最大
- 解码 $y$ 得到 $h(x)$，用 $ED(h(x),l)$ 计算与标签的编辑距离