EM算法应用之GMM和HMM

发表于 | 更新于

几种分布的概念

  • 均匀分布，定义在区间 $[a,b] \ \ (a<b)$ 上连续变量的简单分布，记为 $U(x|a,b)$
  • 0-1 分布（伯努利分布），就是 $n=1$ 情况下的 二项分布
  • 二项分布，重复 n次独立的伯努利分布，每次分布结果只有两种结果且独立
  • 多项式分布，将伯努利分布的结果扩展到多维状态，在此基础上扩展二项分布，就是多项分布
  • 高斯分布(正态分布)，若随机变量 $X$ 服从一个期望为 $\mu$ 、方差为 $\sigma^2$ 的正态分布，记为 $N(\mu, \sigma^2)$ ,当 $\mu=0, \sigma=1$ 时称为标准正态分布
  • 共轭分布，由先验分布于似然分布确定的后验分布与先验分布属于同一种类型的分布，则先验分布为似然分布的共轭分布，也称共轭先验。即先验 $P(\Theta)$ ,似然分布 $P(X|\Theta)$ , 后验分布 $P(\Theta|X)$
  • 高斯分布的共轭是高斯分布，多项分布的共轭是狄利克雷分布，二项分布的共轭是Beta分布
  • 贝叶斯公式： $$P(\Theta|X)=\frac{P(X|\Theta)P(\Theta)}{P(X)}$$

高斯混合模型(GMM)

1、单个高斯模型

定义： $N(\mu, \sigma)$ 模型参数： $\mu$ , $\sigma$ 数据分布： $X={x_1,x_2,...,x_n}$ 如何求模型参数？

  • 定义对数似然函数: $L = \sum_{i=1}^N \log N(x_i|\mu,\sigma)$
  • 求最大值： $L = \arg\max [\sum_{i=1}^N \log N(x_i|\mu,\sigma)]$
  • 分别对 $\mu$ 和 $\sigma$ 求导

2、混合模型

定义（K个高斯）： $P(\Theta)=\sum_{i=1}^{k}\phi_i N(\mu_i, \sigma_i)$ 模型参数: $\Theta = {\mu_1,\mu_2,...,\mu_k,\sigma_1,\sigma_2,...,\sigma_k,\phi_1,\phi_2,...,\phi_k}$ ，并且满足: $\sum_{i=1}^k \phi_i = 1$ 数据分布： $X={x_1,x_2,...,x_n}$ 同理求模型参数：

  • 求最大： $\Theta_{MLE} = \arg\max {\sum_{i=1}^k log P(\Theta) }$
  • 求导很难， $P(\Theta)$ 函数中有 $log$ 加法，难计算
  • 思考，采用迭代法，使用EM算法

EM算法

含隐变量的参数学习算法，应用在GMM中有以下步骤：

    1. 初始化参数 $\Theta^1$
    1. 迭代公式： $\Theta^{g+1}= f(\Theta^g)$ $$\Theta^{g+1}=\arg\max \sum_z \log P(X,Z|\Theta) \cdot P(Z|x,\Theta^g)$$ 保证 $$\log P(X|\Theta^{g+1}) \ge log P(X|\Theta^g)$$ $Z$ 是隐藏变量，也称辅助变量，在高斯混合模型中，可以理解为每个单个的高斯是属于混合高斯中的第 $1 \le Z_i \le k$ 个。$X$ 属于观测值。证明略
    1. 定义 $P(X,Z|\Theta)$ 和 $P(Z|X,\Theta)$ 的计算公式，求期望（E-step）
    1. 分别对所有参数求偏导，求极大值（M-step）
    1. 重复以上计算

EM参考资料

概率图模型

1、马尔可夫链

给定一个概率图，写出其联合概率分布，概率图为 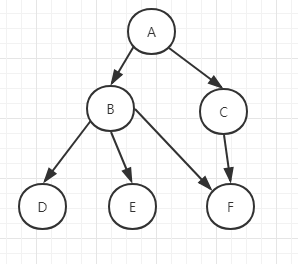马尔可夫链 对应的概率分布为： $$P(A,B,C,D,E,F)=P(D|B)P(E|B)P(F|B,C)P(B|A)P(C|A)P(A)$$ 总结: $P(x_1,x_2,...,x_n)=\prod P(x_i|parents(x_i))$

2、HMM

隐马尔可夫模型是关于时序的概率模型，隐藏的马尔可夫链随机生成的状态的序列，称为状态序列（state sequence），每一个状态生成一个观测，而由此产生的观测的随机序列，称为观测序列（observation sequence）。序列的每一个位置又可以看作是一个时刻。

隐马尔可夫模型有初始概率分布，状态转移分布以及观测概率分布确定。隐马尔可夫模型的形式定义： 设 $Q$ 是所有可能的状态的集合， $V$ 是所有可能观测的集合 $$Q={q_1,q_2,...,q_N}, V={v_1,v_2,...v_M}$$ 其中， $N$ 是可能的状态数， $M$ 是可能的观测数。 $I$ 是长度为 $T$ 的状态序列， $O$ 是对应的观测序列。 $$I={i_1,i_2,...,i_T }, O={o_1,o_2,...,o_T}$$ $A$ 是转移概率矩阵， $B$ 是观测概率矩阵， $\pi$ 是初始化状态概率向量。

隐马尔可夫模型有初始状态概率向量 $\pi$ 、转移概率矩阵 $A$ 和观测概率矩阵 $B$ 决定， $\pi$ 和 $A$ 决定状态序列， $B$ 决定观测序列。因此，隐马尔可夫模型 $\lambda$ 可以用三元符号表示，即: $$\lambda = (A, B, \pi)$$ $A$ ，$B$ ， $\pi$ 称为隐马尔可夫模型三要素。

3、隐马尔可夫模型的3个基本问题

1.概率计算问题

给定模型 $\lambda = (A, B, \pi)$ 和观测序列 $O={o_1,o_2,...,o_T}$ ,求 $P(O|\lambda)$ 方案： 前向后向算法

2、学习问题

给定观测序列 $O={o_1,o_2,...,o_T}$ ，估计模型参数 $\lambda$ ,即求 $P(\lambda|O)$ 概率最大的参数 方案：B-W算法，就是EM算法在HMM中的应用

3、预测问题（也称解码Decoding）

给定模型 $\lambda = (A, B, \pi)$ 和观测序列 $O={o_1,o_2,...,o_T}$ ，求隐藏状态序列 $I^\star$ ,即求 $P(I|O,\lambda)$ 方案：Viterbi算法

4、前向后向算法

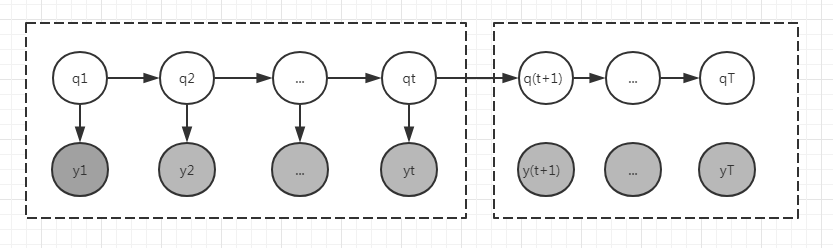前向后向算法 如图所以：前向定义（左） $$\alpha_i(t) = P(y_1,y_2,...,y_t,q_t=i|\lambda)$$ 依据HMM的两个假设以及 $\alpha$ 的定义，可以得出以下递推步骤：

  • 1、 $\alpha_1(i) = \pi_i b_i(o_1)$ $i=1,2,..,N$
  • 2、递推，对 $t=1,2,..,T-1$ , $$\alpha_{t+1}(i)=b_i(o_{i+1}) \sum_{j=1}^N \alpha_t(i) a_{ji}$$ $i=1,2,...,N$
  • 3、终止 $$P(O|\lambda)=\sum_{i=1}^N \alpha_T(i)$$

后向定义（右） $$\beta_i(t)=P(y_{t+1},...,y_T|q_t=i, \lambda)$$ 同理可以得出后向递推步骤：

  • 1、 $\beta_T(i)=1, i=1,2,...,N$
  • 2、对 $t=T-1,T-2,...,1$ $$\beta_t(i)=\sum_{j=1}^N a_{ij} b_j(o_{t+1})\beta_{t+1}(i),i=1,2,..,N$$
  • 3、终止 $$P(O|\lambda)=\sum_{i=1}^N \pi_i b_i(o_1) \beta_1(i)$$

5、B-W算法

  • 1、确定完全数据的对数似然函数 所有观测数据 $O={o_1,o_2,...,o_T}$ ，所有隐含数据 $I={i_1,i_2,...,i_T}$ ，完全数据是 $(O,I)=(o_1,o_2,..,o_T,i_1,i_2,...,i_T)$ 。完全数据的对数似然函数是 $log P(O,I|\lambda)$
  • 2、EM算法的E步：求 $Q$ 函数 $Q(\lambda, \bar \lambda)$ 根据EM的定义， $$Q(\lambda, \bar \lambda)=\sum_I \log P(O,I|\lambda) P(O|I,\bar \lambda)$$ 依据贝叶斯可以直接写成 $$Q(\lambda, \bar \lambda)=\sum_I \log P(O,I|\lambda) P(O,I|\bar \lambda)$$ 其中 $\bar \lambda$ 是隐马尔科夫模型参数的当前估计值（是个常数）， $\lambda$ 是要极大化的隐马尔科夫模型参数
  • 3、因为马尔可夫有以下计算公式： $$P(O,I|\lambda)=\pi_{i_1}b_{i_1}(o_1)a_{i_1 i_2}b_{i_2}(o_2) \cdot \cdot \cdot a_{i_{T-1}}b_{i_T}(o_T)$$ 做对数似然之后就变成了逐项求和
  • 4、EM算法的M步：利用拉格朗日乘子法对参数 $\lambda$ 求导估计

B-W算法参考资料

6、预测算法（Viterbi）

采用Viterbi算法，利用动态规划求概率最大路径(最优路径)。这时一条路径对应着一个状态序列。《统计学习方法》p.185，p.186 算法描述:

  • 输入：模型 $\lambda = (A, B, \pi)$ 和观测 $O=(o_1,o_2,...,o_T)$
  • 输出：最优路径 $I^=(i_1^,i_2^,...,i_T^)$ .
(1) 初始化

$$\delta_1(i)=\pi_i b_i(o_1), i=1,2,...,N \ \psi_1(i)=0, i=1,2,...,N$$

  • $\delta_1(i)$ 表示 $t=1$ 状态 $i=1,2,...,N$ 分别的最大概率
  • $\psi_1(i)$ 表示 $t=1$ 所有状态序列 $I=(i_1,i_2,...,i_{t-1},i)$ 中概率最大的是第 $t=t-1$ 个节点，这里 $t-1=0$
(2) 递推，对 $t=2,3,...,T$

$$\delta_1(i)=\max_{1\leq j\leq N}[\delta_{t-1}(j)a_{ji}]b_i(o_t),i=1,2,...,N \ \psi_t(i)=\arg \max_{1\leq j\leq N}[\delta_{t-1}a_{ji}],i=1,2,...,N$$

(3) 终止

$$P^\star=\max_{1\leq j\leq N} \delta_T(i) \ i_T^\star=\arg \max_{1\leq j\leq N}[\delta_T(i)]$$

(4) 最优化路径回溯. 对 $t=T-1,T-2,...,1$

$$i_t^\star=\psi_{t+1}(i_{t+1}^\star)$$ 求得最优路径 $I^\star=(i_1^\star,i_2^\star,...,i_T^\star)$

因为最近做了CTC_Viterbi解码，所以写了一个Viterbi解码的示例代码，实现了书中盒子的问题

代码实现： 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
# HMM viterbi 书上例子实现
def HMM_viterbi():
    A = np.asarray([[0.5, 0.2, 0.3], [0.3, 0.5, 0.2], [0.2, 0.3, 0.5]])
    B = np.asarray([[0.5, 0.5], [0.4, 0.6], [0.7, 0.3]])
    Pi = np.asarray([0.2, 0.4, 0.4]).transpose()

    O = np.asarray([0,1,0])  # O = [红， 白， 红]
    T = O.shape[0]   # len(O)
    N = A.shape[0]   # 状态数

    Vi = np.zeros([T, N])
    Path = np.zeros([T, N], dtype=np.int16)
    # 步骤（1）初始化
    Vi[0, :] = Pi * B[:, 0]
    print(Vi)
    
    for t in range(1, T):
        # 步骤（2）递推
        for i in range(N):
            p_news = []
            for j in range(N):
                p_trans = A[j,i]
                p_outs = B[i,O[t]]    # 这儿是个易错点,主要观测 O=(0,1,0)，要和B对应起来考虑
                p_delta = Vi[t-1, j]
                p_news.append(p_delta*p_trans*p_outs)
 
            Vi[t, i] = np.max(p_news)
            Path[t, i] = np.argmax(p_news)
    
    # 步骤（3）终止
    P = np.max(Vi[T-1])
    i_star = np.argmax(Vi[T-1])
    # 步骤（4）最优路径回溯
    best_path = np.zeros([T], dtype=np.int16)
    best_path[T-1] = i_star
    
    for t in range(T-2, -1, -1):
        best_i = Path[t+1][i_star]
        best_path[t] = best_i
        i_star = best_i
    
    print(Vi)
    print(best_path)
    return Vi, best_path
            
HMM_viterbi()

# 结果
[[0.1  0.16 0.28]
 [0.   0.   0.  ]
 [0.   0.   0.  ]]
[[0.1     0.16    0.28   ]
 [0.028   0.0504  0.042  ]
 [0.00756 0.01008 0.0147 ]]
[2 2 2]

7、Viterbi强制解码

解码过程：

  • 输入：RNN特征经过一层softmax的结果 $y$ 和 labels。 $y$ 的shape是: [300,62]，300帧的音频，音素词表大小是62(包含blank) labels是加完blank后的列表 labels=[0,5,0,5,0,6]，真实label=[5,5,6]
  • 输出：最优结果，得分（最大概率）

过程(参考前向概率算法)：

  • 初始化： Vi[0,0] = y[0,labels[0] Vi[0,1] = y[0,labels[1]
  • 递推： Vi[t, i] = max{Vi[t-1, i], Vi[t-1, i-1]} * y[t, labels[i]]

代码和结果(随机生成10组特征值) 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
# viterbi 解码 参考前向算法
def viterbi_t(y, labels): 
    T, V = y.shape # T 时刻，帧数 ， V 音素
    
    L = len(labels)
    Vi = np.zeros([T, L])
    
    path = np.zeros([T, L], dtype=np.int16)
    # init
    Vi[0, 0] = y[0, labels[0]]
    Vi[0, 1] = y[0, labels[1]]
    
    best_path = [0 for i in range(T)]

    for t in range(1, T):
        for i in range(L):
            if i == 0:
                Vi[t, i] = Vi[t-1, i]*y[t, labels[i]]
                path[t,i] = i
            else:
                Vi[t, i] = max(Vi[t-1, i], Vi[t-1, i-1])* y[t, labels[i]]
                path[t, i] = i if Vi[t-1,i] > Vi[t-1, i-1] else i-1
    
    score = np.max(Vi[T-1])
    p = np.argmax(Vi[T-1])
    
    best_path[T-1] = p
    for i in range(T-2,-1,-1):
        best_i = path[i+1][p]
        best_path[i] = best_i
        p = best_i
    
    return Vi,best_path,score

# 0 for blank
labels = [0, 5, 0, 5, 0, 6, 0]
# labels = [0, 5, 6, 7, 8, 0]  
print('labels:', labels)
print('最优路径------------------输出结果------------------最大概率')
for k in range(10):
    np.random.seed(k)
    y = softmax(np.random.random([30, 62]))
    Vi,max_p,score = viterbi_t(y, labels)
    pas = [labels[i] for i in max_p]
    print(max_p,remove_blank(pas), score)

1
2
3
4
5
6
7
8
9
10
11
12
labels [0, 5, 0, 5, 0, 6, 0]
最优路径------------------输出结果-------------------最大概率
[0, 0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 1, 2, 2, 2, 2, 3, 3, 3, 4, 5, 5, 5, 5, 5, 6, 6, 6, 6, 6] [5, 5, 6] 1.3673497237243052e-52
[0, 0, 0, 0, 0, 0, 1, 2, 2, 2, 2, 2, 3, 3, 3, 3, 3, 4, 5, 5, 5, 5, 5, 5, 5, 6, 6, 6, 6, 6] [5, 5, 6] 1.395352642036245e-52
[0, 0, 1, 2, 2, 2, 2, 2, 3, 4, 4, 4, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 6, 6, 6, 6] [5, 5, 6] 3.2977391549480784e-53
[0, 0, 0, 0, 0, 0, 1, 1, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 3, 3, 3, 4, 4, 4, 4, 5, 5, 5] [5, 5, 6] 1.517799502424806e-52
[0, 0, 0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 2, 2, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 4, 5, 5, 5, 5, 5] [5, 5, 6] 5.656781395271036e-54
[0, 0, 1, 2, 2, 2, 3, 3, 3, 3, 4, 4, 4, 5, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6] [5, 5, 6] 1.767851623254299e-52
[0, 0, 0, 1, 2, 3, 4, 4, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 6, 6, 6, 6] [5, 5, 6] 2.363012737251222e-52
[1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 2, 2, 2, 2, 2, 2, 2, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3] [5, 5] 1.7363478260931123e-53
[0, 0, 1, 1, 2, 2, 2, 2, 2, 2, 3, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 5, 5, 5, 5, 5, 5, 5, 6] [5, 5, 6] 1.2178289029142287e-53
[0, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 2, 2, 2, 2, 3, 3, 3, 3, 3, 3, 3, 3] [5, 5] 5.254795879619996e-53

第三代语音识别 GMM+HMM

参考资料：